Koen Derks

In 1938 toonde Frank Benford aan dat in veel natuurlijk voorkomende gegevens het cijfer 1 vaker als eerste cijfer voorkomt dan een 2, een 2 vaker dan een 3, enzovoort¹. Dit komt doordat tellingen vaak beginnen bij lage getallen en niet altijd doorlopen tot hoge getallen. Hierdoor komen cijfers zoals 1 vaker voor dan bijvoorbeeld 9, zoals bij bevolkingsaantallen van landen. Hetzelfde patroon is ook terug te zien bij processen waarbij waarden op multiplicatieve wijze groeien, zoals bij aandelenkoersen. Dit fenomeen, bekend als de Wet van Benford, kan gelden als een gouden standaard voor de 'natuurlijkheid' van bepaalde gegevens.

De Wet van Benford kent toepassingen binnen de audit. Om mogelijke fraude op te sporen stelde Nigrini (1992) bijvoorbeeld voor om te toetsen of de eerste (of eerste twee) cijfers van bedragen in overeenstemming zijn met de Wet van Benford. Dit is tegenwoordig een standaard onderdeel van veel controles (zie bijvoorbeeld Touw en Hoogduin, 2012, Hoofdstuk 11). Hoewel deze analyse in geen enkele mate bewijs voor of tegen fraude biedt (een fraudeur die de Wet van Benford kent, kan hierop anticiperen), kan het wel richting geven aan vervolgwerkzaamheden.

De Wet van Benford is opgenomen in veel auditsoftwarepakketten. Helaas kosten deze pakketten geld en analyseren ze vaak alleen bedragen. De wet is echter ook toepasbaar op andere gegevens, zoals geregistreerde kilometers, gewerkte uren en de duur van inlogsessies². In deze column laat ik zien ik hoe je met de auditmodule in het gratis open-source statistiekprogramma JASP (JASP Team, 2025) de Wet van Benford kunt toetsen. Zo kun je de regie in eigen hand nemen en de wet zelf op diverse gegevens toetsen.

De Wet van Benford

Voordat ik een voorbeeld bespreek, leg ik eerst kort de wiskunde uit. De Wet van Benford stelt dat in natuurlijk voorkomende gegevens de kans op een specifieke reeks van eerste cijfers volgens een logaritmische verdeling afneemt. Concreet betekent dit bijvoorbeeld dat het cijfer d als eerste cijfer voorkomt met een kans log₁₀(1 + 1/d)³. Door d = 1 in te vullen krijg je 0,301, oftewel 30,1 procent en hetzelfde kan worden gedaan voor de cijfers d = 2, 3, …, 9, zoals weergegeven in de onderstaande figuur.

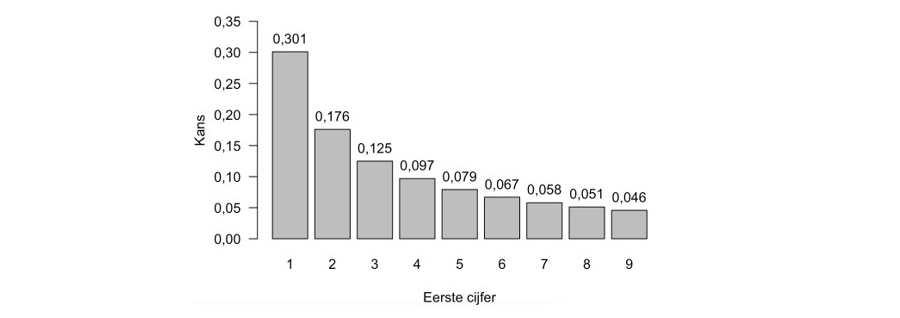
De kansen in de figuur kun je zien als de verwachte relatieve frequenties van de eerste cijfers. Bij een dataset kun je de waargenomen relatieve frequenties berekenen door simpelweg de eerste cijfers van elke waarneming te tellen en deze aantallen te delen door het totale aantal waarnemingen. Bij 'natuurlijke' gegevens verwacht je een kleine afwijking tussen de verwachte en waargenomen relatieve frequenties. Bij vervalste gegevens is het idee dat deze afwijking groter is.

Voorbeeld

Ik gebruik in deze column een fictief voorbeeld, waarin je de juistheid van de rittenregistratie van een mkb-bedrijf controleert, bestaande uit 1.160 zakelijke ritten. De onderstaande tabel toont de verdeling van de eerste cijfers van de geregistreerde privé-omrijkilometers⁴. De tweede en derde kolom geven de waargenomen (relatieve) frequenties weer en de vierde kolom toont de verwachte relatieve frequenties volgens de Wet van Benford. De laatste kolom bevat de afwijking tussen de verwachte en waargenomen relatieve frequenties.

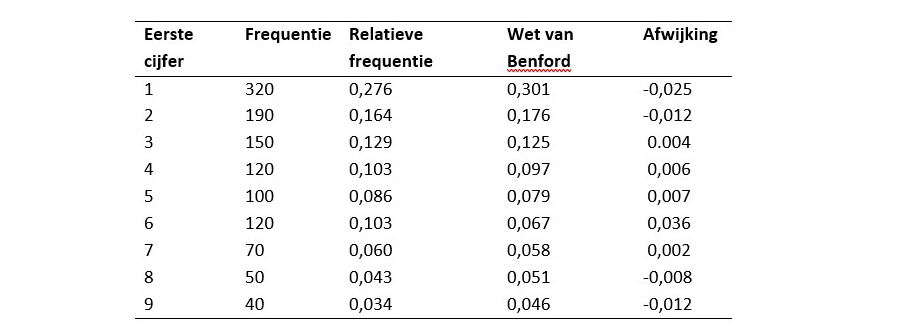
Om te bepalen of de afwijkingen in de laatste kolom groot genoeg zijn om te concluderen dat de geregistreerde privé-omrijkilometers afwijken van de Wet van Benford, moet je een statistische toets gebruiken. Voor deze toets gebruik je in dit voorbeeld een betrouwbaarheid van 95 procent (α = 0,05).

Handmatig zou je eerst de tabel moeten maken en vervolgens de chi-kwadraat statistiek berekenen⁵ om de significantie te bepalen (Touw en Hoogduin, 2012, Hoofdstuk 11). Als de significantie lager is dan α, verwerp je de hypothese van conformiteit en concludeer je dat de geregistreerde privé-omrijkilometers niet in overeenstemming zijn met de Wet van Benford. De audit module van JASP (JASP for Audit) doet dit allemaal automatisch voor je en documenteert de analyse in een auditrapport. 

Toetsen van de Wet van Benford met JASP for Audit

Om de Wet van Benford met JASP for Audit te toetsen, download en installeer je eerst JASP. Stel via het menu in de linkerbovenhoek (Preferences - Interface - Preferred language) de interface en resultaten in het Nederlands in. Laad vervolgens het gegevensbestand⁶ in JASP en schakel de auditmodule in door op het '+'-symbool in de rechterbovenhoek te klikken en 'Audit' te selecteren. De module verschijnt dan in het menu bovenaan het scherm.

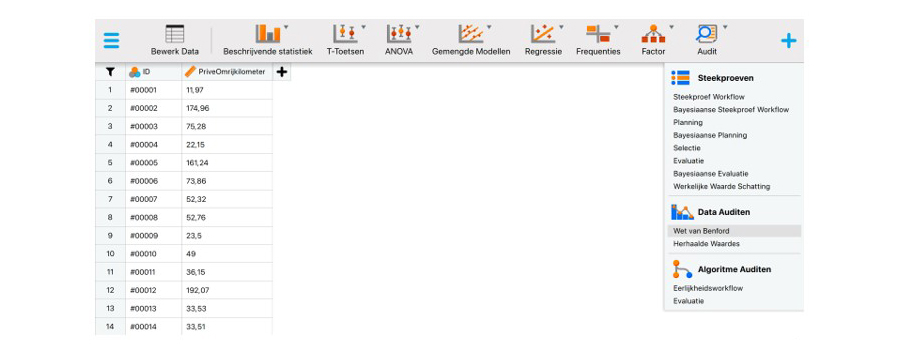
Klik op de audit module en open de analyse 'Wet van Benford'. Sleep in de interface de variabele PriveOmrijkilometer naar het vak 'Variabele'. Selecteer vervolgens in de sectie 'Rapport' de figuur 'Waargenomen vs. verwacht'. Hiermee vraag je een figuur op die de waargenomen en verwachte relatieve frequenties toont en afwijkingen van de Wet van Benford markeert⁷.

Resultaten

Na het invullen van de opties berekent JASP for Audit automatisch de resultaten en toont de onderstaande tabel. De eerste kolom (n = 1.160) toont het aantal geregistreerde ritten. De tweede kolom bevat de gemiddelde absolute afwijking (Mean Absolute Deviation, MAD = 0,013) van de waargenomen ten opzichte van de verwachte relatieve frequenties. Een lagere MAD betekent kleine afwijkingen, een hogere MAD grotere afwijkingen⁸. De derde, vierde en vijfde kolommen tonen respectievelijk de chi-kwadraat statistiek (X² = 32,738), het aantal vrijheidsgraden (df = 8) en de significantie (p < ,001). Omdat de significantie kleiner is dan α = 0,05, kun je in dit voorbeeld concluderen dat de geregistreerde privé-omrijkilometers niet in overeenstemming zijn met de Wet van Benford.

Nu je hebt geconcludeerd dat de rittenregistratie niet voldoet aan de Wet van Benford, wil je weten welke eerste cijfers afwijken. De onderstaande figuur uit JASP for Audit toont de waargenomen relatieve frequenties van de eerste cijfers (blauwe stippen) en de verwachte relatieve frequenties volgens de Wet van Benford (grijze balken). De rode balk geeft aan dat privé-omrijkilometers met het eerste cijfer 6 significant vaker voorkomen dan verwacht⁹.

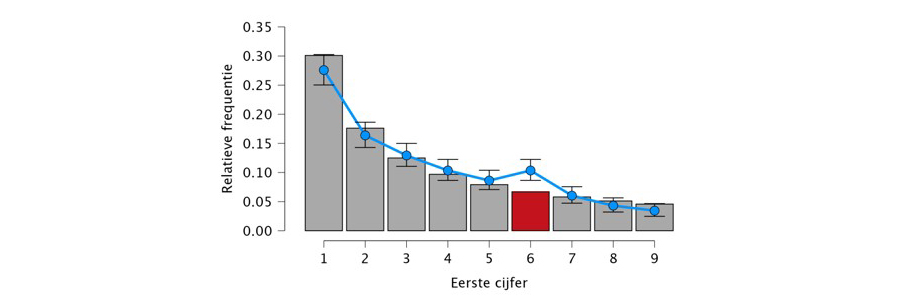
Door op de knop 'Download Rapport' te klikken, exporteer je deze resultaten met bijbehorende uitleg naar een auditrapport. Zo heb je de analyse meteen netjes gedocumenteerd.

Om te illustreren dat 'natuurlijke' gegevens wel kunnen voldoen aan de Wet van Benford, heb ik nog een ander fictief gegevensbestand met een rittenregistratie online beschikbaar gemaakt¹⁰. In deze rittenregistratie zijn de privé-omrijkilometers tot stand gekomen door per rit een afwijking van de meest gebruikelijke zakelijke route te simuleren, waarbij deze afwijking na elke gereden kilometer met 1 procent kans wordt beëindigd. Dit is een natuurlijk proces en de resulterende gegevens voldoen dan ook aan de Wet van Benford. Ik nodig de geïnteresseerde lezer uit om dit zelf te verifiëren met JASP for Audit.

Vervolgwerkzaamheden

De resultaten van de voorgaande analyse kun je gebruiken om de controle van de rittenregistratie verder in te richten. Controleer bijvoorbeeld de ritten waarvan het aantal geregistreerde privé-omrijkilometers met het cijfer 6 begint intensiever, omdat deze vaker voorkomen dan verwacht. Zo gebruik je de analyse om focus aan te brengen in je vervolgwerkzaamheden.

Tot slot is het belangrijk om nogmaals te benadrukken dat het toetsen van de Wet van Benford geen bewijs voor of tegen fraude levert. Afwijkingen van de Wet van Benford betekenen niet automatisch dat er sprake is van fraude. Het kan bijvoorbeeld zijn dat werknemers vaak bij één bepaalde supermarkt boodschappen doen, die zes kilometer van de gebruikelijke route gelegen is. Andersom betekent conformiteit met de wet niet dat er geen fraude is. Zoals eerder vermeld kan een fraudeur namelijk ook anticiperen op deze analyse. Het is daarom verstandig om de Wet van Benford alleen te gebruiken om richting te geven aan eventuele vervolgwerkzaamheden.

Voetnoten

1. De Wet van Benford werd eigenlijk al in 1881 ontdekt door Simon Newcomb, die zag dat in logaritmetabellen de eerste pagina’s, met getallen die met een 1 begonnen, veel meer versleten waren dan de latere pagina's.

2. Houd er rekening mee dat de Wet van Benford vaak niet van toepassing is op toegekende nummers, zoals ID-nummers, telefoonnummers en postcodes. Deze gegevens zijn daarom niet geschikt voor analyse met de Wet van Benford.

3. Merk op dat de som van deze kansen gelijk aan één is.

4. Privé-omrijkilometers zijn de kilometers die afwijken van de meest gebruikelijke zakelijke route als tijdens een rit zowel zakelijke als privékilometers worden gereden.

5. Je berekent de chi-kwadraat statistiek met de formule X² = ∑((O_i – E_i)² / E_i), waarbij O_i de i-de frequentie in de tweede kolom is en E_i de i-de verwachte relatieve frequentie uit de vierde kolom, vermenigvuldigd met het totale aantal zakelijke ritten. Dit resulteert in X² = 32,738. Ik laat het aan de geïnteresseerde lezer over om deze uitkomst te verifiëren.

6. Het gegevensbestand is hier te vinden.

7. In JASP for Audit kun je deze analyse ook toepassen, om te toetsen of de eerste twee cijfers of het laatste cijfer in overeenstemming zijn met de Wet van Benford, of met een uniforme verdeling.

8. Nigrini (2000) stelt de volgende grenzen voor de MAD voor: nauwe conformiteit (0 - 0,004), acceptabele conformiteit (0,004 - 0,008), marginaal acceptabele conformiteit (0,008 - 0,012), en non-conformiteit (> 0,012). Maar welke grenzen redelijk zijn, is afhankelijk van de steekproefgrootte en aard en context van de gegevens.

9. Dit is gebaseerd op het feit dat de verwachte relatieve frequentie van dit eerste cijfer niet in het 95 procent betrouwbaarheidsinterval voor de waargenomen relatieve frequentie ligt.

10. Dit gegevensbestand is hier te vinden.  

Referenties

• JASP Team. (2025). JASP (Versie 0.95.0)[Computer software].

• Nigrini, M. J. (1992). The Detection of Income Tax Evasion Through an Analysis of Digital Frequencies. PhD thesis, University of Cincinnati, OH, USA.

• Nigrini, M. J. (2000). Digital Analysis Using Benford's Law: Test and Statistics for Auditors. Global Audit Publications.

• Touw, P. & Hoogduin, L. (2012). Statistiek voor Audit en Controlling. Boom, Amsterdam.