Niels van Leeuwen

Rekenbladen en software geven je wel een uitkomst, maar er wordt zelden uitgelegd hoe tot deze uitkomst is gekomen. Instructies en handboeken zijn soms geschreven door collega's die al jaren niet meer werken bij jouw organisatie. Met wat moeilijke termen hier en daar lijkt het wel een mysterie hoe je tot een goed onderbouwde steekproefomvang moet komen. Zonder duidelijke uitleg over hoe je deze omvang berekent is het risico dat je een fout maakt groot. Maar als de methodes helder zijn, dan ontrafelt het mysterie zich en kun je met veel meer vertrouwen gebruik maken van statistiek in je opdracht.

Deze column is onderdeel van een serie van vijf waarin we verschillende steekproefomvang berekeningen behandelen. Deze eerste column is een introductie van kernbegrippen van statistiek en geeft weer welke verschillende berekeningen er zijn. Het doel van deze column is om te begrijpen welke berekeningen je kunt toepassen.

De tweede column laat zien hoe je in Excel een steekproefomvang kunt uitrekenen met verschillende rekenmethodes. Het doel van deze column is dat je zelfstandig kunt komen tot een steekproefomvang. De derde column laat zien hoe je in bepaalde gevallen zelfs handmatig een steekproefomvang kunt berekenen. Het doel hiervan is een beter begrip te geven van de formules die je in Excel hebt gebruikt bij de vorige column. De vierde column laat zien hoe je middels algoritmes in VBA de berekeningen kunt automatiseren. Het doel hiervan is inzicht te geven hoe software tot een bepaalde steekproefomvang komt, zodat je hier met voldoende vertrouwen op kunt steunen. De vijfde en laatste column laat zien hoe je deze berekeningen in het (gratis) open source softwarepakket JASP kunt uitvoeren.

Het doel van de gehele serie is dat je kennis opdoet van de meest gebruikte berekeningen om te komen tot een steekproefomvang en in staat bent deze zelfstandig uit te voeren. Je kunt hierdoor de uitgangspunten die je doet bij het opstellen van een steekproefomvang-berekening goed onderbouwen.

Audit en statistiek

Laten we eerst kijken naar de relatie tussen audit en statistiek. Als auditor willen we met voldoende mate van zekerheid een conclusie trekken dat een object van onderzoek vrij is van materiële fouten of onzekerheden. De statistiek leert ons hoe wij met een steekproef met een beperkt aantal waarnemingen met voldoende betrouwbaarheid een conclusie kunnen trekken over een populatie. Beide invalshoeken komen samen tot één definitie van het doel van steekproeven in de audit. We willen dan met een beperkt aantal waarnemingen met voldoende betrouwbaarheid de conclusie trekken dat een object van onderzoek vrij is van materiële fouten en onzekerheden. De vraag die je hierbij kunt stellen is: bij hoeveel waarnemingen kan ik met voldoende zekerheid een uitspraak doen? Dit is waar statistische berekeningen om de hoek komen.

Soorten berekeningen

Er zijn verschillende manieren om tot een steekproefomvang te komen. Statistiek is een breed vakgebied. Voor specifieke vraagstukken bestaan ook specifieke oplossingen. Dit geldt ook voor de toepassing van statistiek in de audit. Om een goed beeld te krijgen van deze verschillende manieren gaan we eerst in op het verschil tussen continue en discrete data. Als we dit hebben gedaan kunnen we ons een goed beeld vormen van welke methodes dan van toepassing zijn op audits.

Discrete en continue data
De normale verdeling is het meest onderwezen model in de statistiek. Maar voor ons onderwerp is dit model minder goed van toepassing. Het kenmerkende van de normale verdeling is de klokvormige kansverdeling, waarbij veel waarnemingen rond het gemiddelde vallen en de kans op waarnemingen die van het gemiddelde af liggen steeds verder afneemt. Deze gemiddeldes en afwijkingen kun je opdelen in steeds kleinere stukjes. De normale verdeling is om deze reden een verdeling gebaseerd op continue data. In plaats van het meten of iets dicht bij het gemiddelde valt, willen we bij de audit weten of onze waarnemingen goed of fout zijn. We classificeren dus data en dat is iets wezenlijk anders. Informatie met classificaties zoals goed of fout noemen we discrete data. Voor ons vraagstuk moeten we dus berekeningen zoeken die discrete data behandelen.

In de statistiek denkt men bij discrete data bijvoorbeeld aan een zak knikkers met twee of meer kleuren. Om deze berekeningen toe te kunnen passen moeten we eerst de aanname doen dat onze populatie vergelijkbaar is met een zak knikkers met twee kleuren. Onze populatie is dan een zak euro's met twee mogelijke eigenschappen: goed of fout gepresenteerde euro's. Met deze aanname kunnen we verder kijken naar welke berekeningen toepasbaar zijn.

Toepasbare berekeningen
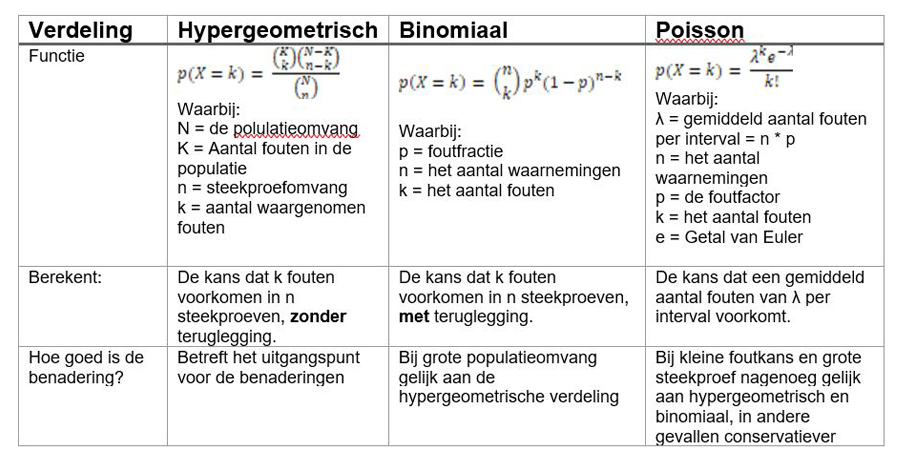
Er zijn tal van discrete verdelingen, maar drie zijn goed toepasbaar voor de audit. Dit zijn de hypergeometrische verdeling, de binomiale verdeling en de Poisson-verdeling. De reden dat specifiek deze drie verdelingen goed passen, is omdat al deze drie verdelingen kijken naar meerdere waarnemingen die te classificeren zijn in twee groepen. Er zijn namelijk ook verdelingen die kijken naar meer dan twee mogelijkheden, wat voor ons vraagstuk niet relevant is.

Voor iedere verdeling bestaan goede argumenten om deze te gebruiken. Het hangt allemaal af van de aard van de verdeling die je neemt en hoe zich dat verhoudt tot wat wij in de audit doen. Laten we hier per verdeling wat dieper op ingaan.

Hypergeometrische verdeling
De hypergeometrische verdeling kijkt naar meerdere waarnemingen die goed of fout kunnen zijn en gaat ervan uit dat je waarnemingen niet terug stopt in je populatie voordat je een nieuwe waarneming doet. Dit wordt zonder teruglegging genoemd. Dit is de meest passende verdeling voor wat we in de audit doen. Je controleert namelijk een selectie van euro's die je beoordeelt en vervolgens op een aparte lijst bijhoudt. Je stopt de waarnemingen niet meer terug in de populatie en hebt zo dus ook niet de kans dat je dezelfde post dubbel trekt. Deze methode vertoont de meeste overeenkomsten met wat we daadwerkelijk in de audit doen. Echter er bestaan relatief weinig rekenmethodes voor de berekening van de steekproefomvang.

Binomiale verdeling
Bij de binomiale verdeling is ook sprake van waarnemingen die in goed of fout worden geclassificeerd, maar bij deze verdeling is er wel sprake van teruglegging. Als je dit letterlijk zou toepassen binnen de audit, dan zou je een post op een willekeurige manier moeten selecteren, controleren of deze goed of fout is en dan vervolgens terug stoppen in je populatie van posten. Hierna neem je weer een willekeurige waarneming, met de kans dat je dezelfde post trekt. Deze methode lijkt erg op wat we daadwerkelijk in de audit doen met het verschil dat we meestal niet terugleggen in de audit. Ook hier bestaan relatief weinig rekenmethodes voor de berekening van de steekproefomvang.

De Poisson-verdeling
Bij de Poisson-verdeling kijk je niet naar een waarneming los, maar naar een telling van het aantal fouten per interval. Deze verdeling is bedacht om tellingen te doen in de tijd, bijvoorbeeld hoeveel auto's een kruispunt in één uur passeren. In de audit kunnen wij dit vertalen naar hoeveel foute euro's we vaststellen in vaste intervallen van euro's in de populatie. Hoewel er bij toepassing van de Poisson-verdeling in de literatuur niet vaak wordt gesproken over teruglegging, kun je aannemen dat hier wel sprake is van teruglegging, omdat eenzelfde auto ook meerdere keren over een kruispunt kan rijden.

Voor de Poisson-verdeling is de berekening van de steekproefomvang relatief eenvoudig ten opzichte van die voor de hypergeometrische of binomiale verdeling. Toepassing vraagt echter een vertaling van aantallen fouten naar het aantal foute euro's per interval.

Verschillen beperkt

We zijn ingegaan op de verschillen tussen de drie methodes. Echter in de uitwerking naar berekening van de steekproefomvang voor de audit zijn de verschillen beperkt. Dat komt omdat, zeker voor situaties met een klein aantal verwachte fouten en een grote steekproefomvang, de kansverdelingen nagenoeg aan elkaar gelijk zijn. Gevolg is dat je voor elk van de drie methodes op nagenoeg dezelfde steekproefomvang uitkomt. Echter, wanneer het verwachte aantal fouten groot is en de steekproefomvang klein, dan levert de Poisson-berekening een grotere hoeveelheid steken dan de andere twee. Je verkrijgt dan feitelijk te veel zekerheid ten opzichte van toepassing van de binomiale en hypergeometrische steekproefomvang. Meer zekerheid is echter geen probleem in de audit en dus kun je alle drie de methodes gebruiken. Nu we een goed beeld hebben van de verschillende berekeningen die er zijn zullen we in een volgende column in gaan op de vraag hoe je zelfstandig de juiste steekproefomvang kunt berekenen.

In de onderstaande tabel is dit samenvattend weergegeven en is de functie per verdeling weergegeven.