Een accountant vroeg mij hoe mijn verkeerslichtmodel rijmt met COS 530 A22. Dat gold met name voor de volgende zin: "Hoe kleiner het verschil tussen de (..) geprojecteerde afwijking(..) en (..) de toelaatbare afwijking (..), des te groter is de waarschijnlijkheid dat de werkelijke afwijkingen in de populatie de toelaatbare afwijking overschrijden."

Immers, het verkeerslichtmodel vergelijkt de maximale afwijking met de uitvoeringsmaterialiteit terwijl in COS 530 de geprojecteerde afwijking met de toelaatbare afwijking wordt vergeleken.

Aan de hand van twee getallenvoorbeelden zal ik laten zien dat aan de hand van de toelaatbare afwijking geen steekproef kan worden opgezet (de steekproefomvang is namelijk altijd 1) en geen steekproef kan worden geëvalueerd (het steekproefrisico is namelijk nog te hoog). En dus heeft die alinea geen nut. Ten slotte laat ik in een getalenvoorbeeld zien dat COS 530 A22 niet onwaar is. Dat de tekst verwarrend is, blijkt al aan het grote aantal (..) dat ik in slechts een zin van de hele paragraaf heb moeten aanbrengen om hem leesbaar te maken. 

Het verkeerslichtmodel

Mijn verkeerslichtmodel gaat uit van de begrippen maximale afwijking en geprojecteerde afwijking. De maximale afwijking staat niet in de COS. Maar de COS noemt wel het steekproefrisico. Dat is de kans dat de steekproef ten onrechte tot goedkeuring leidt doordat de werkelijke afwijking hoger is dan toegestaan. De geprojecteerde afwijking is wel in de COS terug te vinden: de meest waarschijnlijke schatting van het bedrag aan afwijkingen in de populatie, gegeven de bevindingen in de steekproef. De maximale afwijking is ook een schatting van het bedrag aan afwijkingen in de populatie, maar die is zo hoog dat er maar een kleine kans is (het steekproefrisico) dat dat bedrag nog hoger had moeten zijn.

Het model heb ik al eens in eerdere blogs (bijvoorbeeld op Accountant.nl) beschreven, en kent drie situaties:

• Groen: goedkeuren wanneer de maximale afwijking onder de uitvoeringsmaterialiteit ligt en de geprojecteerde afwijking ter correctie is voorgelegd om vervolgens het niet gecorrigeerde deel te accumuleren bij de overall evaluatie.
• Oranje: pas goedkeuren als de gecontroleerde de geprojecteerde afwijking corrigeert, wanneer het verschil tussen maximale en geprojecteerde afwijking onder de uitvoeringsmaterialiteit ligt.
• Rood: werkzaamheden uitbreiden totdat het verschil tussen maximale en geprojecteerde afwijking onder de uitvoeringsmaterialiteit ligt om de noodzakelijke correctie te kunnen schatten.

Nu de voorbeelden van het gebruik van de geprojecteerde afwijking. 

Voorbeeld 1 (opzet)

Gegeven zijn: uitvoeringsmaterialiteit 3 procent, toelaatbare afwijking 2 procent, 95 procent betrouwbaarheid.

De controleur wil dus goedkeuren bij 95 procent zekerheid dat de afwijking in de populatie onder 3 procent ligt en bouwt uit voorzorg een buffer in door de steekproef op te zetten met de eis dat 95 procent zekerheid moet worden bereikt dat de afwijking in de populatie onder 2 procent ligt. Deze voorzorg levert een grotere steekproef op, maar bij het vinden van een of meer afwijkingen kan wellicht toch nog worden goedgekeurd. Bij die aangescherpte norm voor de populatie gaat de controleur ervan uit geen afwijkingen in de steekproef te zullen aantreffen.

Een steekproef van 1 waarneming met 0 afwijkingen geeft een geprojecteerde afwijking van 0 procent, en dan is het verschil met de toelaatbare afwijking 2 procent en met de uitvoeringsmaterialiteit 3 procent. Ruim voldoende, dus…? Een steekproef opzetten met behulp van een eis aan de geprojecteerde afwijking kan niet, want dat levert altijd een noodzakelijke omvang op van 1. 

Voorbeeld 2 (evaluatie)

Gegeven zijn: uitvoeringsmaterialiteit 3 procent, toelaatbare afwijking 2 procent, 95 procent betrouwbaarheid. In de steekproef is één (hele) afwijking aangetroffen.
Bij welk aantal waarnemingen is het steekproefrisico tot een aanvaardbaar laag niveau teruggebracht?

Een steekproef van vijftig waarnemingen met 1 afwijking geeft een geprojecteerde afwijking van 2 procent en dan is het verschil met de toelaatbare afwijking nihil, terwijl dat verschil zo moet zijn dat het steekproefrisico aanvaardbaar klein is. De steekproef moet dus groter zijn dan vijftig, maar hoeveel groter? Zullen we er maar honderd doen? De geprojecteerde afwijking is dan 1 procent en dat is onder 2 procent, maar is dat verschil voldoende? Berekening van de maximale afwijking geeft het antwoord.

Een steekproef van 100 met 1 afwijking geeft een geprojecteerde afwijking van 1 procent en een 95 procent betrouwbare maximale afwijking van 4,75/100 = 4,75 procent. Het steekproefrisico dat de werkelijke afwijking in de populatie hoger is dan 4,75 procent is 5 procent, dus de kans dat die afwijkingen de toelaatbare afwijking van 2 procent overschrijden is zeker groter dan 5 procent. Hoeveel groter is te berekenen: omdat de 60 procent betrouwbare maximale afwijking bij honderd waarnemingen met 1 afwijking 2 procent is, is het steekproefrisico 40 procent.

Bij 160 waarnemingen met 1 afwijking is de geprojecteerde afwijking 1/160 en de 95 procent betrouwbare maximale afwijking 4,75/160 = 3 procent. Er is dus nu een kleine (5 procent) kans op ten onrechte goedkeuren. Vergelijking van de maximale afwijking met de uitvoeringsmaterialiteit geeft dus een objectieve maatstaf.

Het is dus ook niet mogelijk om een steekproef te evalueren met behulp van de geprojecteerde afwijking, want het steekproefrisico is daarbij veel te hoog. De maximale afwijking is nodig om het steekproefrisico tot een aanvaardbaar laag niveau terug te brengen.

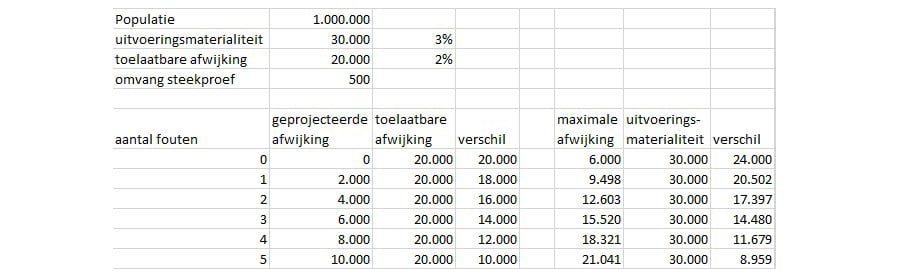
Is de COS tekst nu onwaar? Nee, want als je meer afwijkingen vindt in een steekproef zal zowel de afstand tussen geprojecteerde afwijking en toelaatbare afwijking als de afstand tussen maximale afwijking en uitvoeringsmaterialiteit kleiner worden, zolang die norm nog niet is overschreden. Bijgaand getallenvoorbeeld laat dat zien. Beide maatstaven geven dus aan dat bij meer afwijkingen ook meer waarnemingen nodig zijn.