In een vorige column heb ik een advies gegeven voor het bepalen van de toelaatbare afwijking als percentage van de uitvoeringsmaterialiteit. Door voor 80 procent te kiezen wordt een grotere steekproef gecontroleerd dan strikt noodzakelijk is, maar die steekproef hoeft pas te worden uitgebreid als daarin meer dan één (1) volledige afwijking wordt gevonden.

Nu wil ik een advies geven voor de afslag van overall materialiteit naar uitvoeringsmaterialiteit, door het model van Stewart (2012) te combineren met dat van Glover e.a.(2008). Mijn advies komt neer op het hanteren van een gelijk bedrag aan uitvoeringsmaterialiteit per component. Het hanteren van afzonderlijke bedragen per component leidt weliswaar tot de theoretisch kleinst mogelijke steekproefomvang, maar vereist een complexe berekening. De methode die ik adviseer is effectief (de overall maximale afwijking ligt onder de overall materialiteit) en maakt die complexe berekening overbodig. En, er is meer goed nieuws, maar dat bewaar ik tot het einde.

COS 530 A3 geeft aan dat de accountant de toelaatbare afwijking moet bepalen, en wel in twee stappen:

• 1e afslag: van materialiteit naar uitvoeringsmaterialiteit om het aggregatierisico op te vangen; deze afslag is verplicht zodra er sprake is van (dis-)aggregatie;
• 2e afslag: van uitvoeringsmaterialiteit naar toelaatbare afwijking om ruimte te maken voor het vinden van afwijkingen; deze afslag is niet verplicht, omdat heel vaak geen afwijkingen worden verwacht.

In deze column doe ik een suggestie voor de omvang van die eerste, verplichte, afslag: de vertaling van overall materialiteit naar uitvoeringsmaterialiteit. 

Aggregatiemodellen van Glover en Stewart

Startpunt van beide modellen is het steekproefrisico; dat is de kans dat de maximale afwijking de materialiteit overschrijdt. De geprojecteerde afwijking is de meest waarschijnlijke uitkomst van het bedrag aan afwijkingen in de populatie gegeven de bevindingen in de steekproef. De maximale afwijking is ook een geschat bedrag aan afwijkingen in de populatie, maar dat bedrag is zo hoog dat er maar een kleine kans is (het steekproefrisico) dat die schatting nog hoger had moeten zijn. In dit plaatje staat horizontaal de onbekende afwijking in de populatie en verticaal de kans op een bedrag aan afwijkingen.

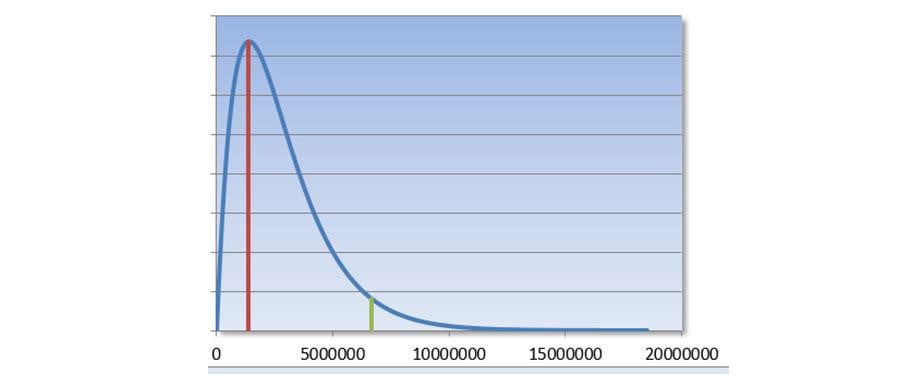
De rode lijn geeft de plek aan van de geprojecteerde afwijking en de groene lijn de maximale afwijking. De oppervlakte rechts van de groene lijn, onder de curve, is het steekproefrisico.

Het aggregatierisico uit COS 600 en COS 320 is het risico dat een materiële afwijking zo is verdeeld over deelpopulaties dat in elke deelpopulatie het bedrag aan afwijkingen te klein is om in de steekproef afwijkingen op te leveren. Het is dus in feite geen aggregatierisico maar een disaggregatierisico. Maar, de oplossing voor de vraag hoe groot de maximale afwijking mag zijn in elke deelpopulatie, oftewel wat de uitvoeringsmaterialiteit per deelpopulatie is, ligt hem in het begrijpen hoe plaatjes zoals hierboven per deelpopulatie optellen tot een plaatje voor de overall populatie.

Glover et al (2008) maken een formule voor het overall steekproefrisico en komen zo tot een tabel. Die geeft aan met welke factor, afhankelijk van het aantal deelpopulaties, de steekproefomvang die voldoende zou zijn als het één populatie betrof moet worden opgehoogd, om daarna naar rato over de delen te worden verdeeld.

Belangrijkste bezwaar tegen deze aanpak is dat de formule gaat over het risico dat de (overall) materialiteit wordt overschreden en niet over de mate waarin de (overall) materialiteit wordt overschreden. Een maximale afwijking van een (1) euro boven de materialiteit telt net zo zwaar mee als een maximale afwijking van tweemaal de materialiteit.

Stewart (2012) maakt een formule voor de overall maximale afwijking in de totale populatie en rekent terug welke uitvoeringsmaterialiteit per deelpopulatie nodig is voor een overall maximale afwijking die aan de overall materialiteit voldoet, en die de kleinste totale steekproefomvang oplevert. Elke deelpopulatie heeft dus een eigen uitvoeringsmaterialiteit. Dat is de schoonheid van zijn model. Dat leidt daardoor tot de kleinste steekproefomvang, maar het rekenwerk is uitermate complex. 

Mijn simplificatie van het model van Stewart

Glover deelt de steekproef naar rato toe over de delen en werkt dus met een vast interval en daarom dus ook met een vast bedrag aan uitvoeringsmaterialiteit. Dat is in feite ook de praktijk bij veel kantoren.
In het model van Stewart is de uitvoeringsmaterialiteit per deelpopulatie alleen een gelijk bedrag als alle deelpopulaties even groot zijn. Het totaal van alle steekproeven op alle deelpopulaties is dan met de vaker gebruikte GAMMA.INV functie van Excel te bepalen.

Vervolgens blijkt dat die omvang de grootst mogelijke steekproef is die bij welke opdeling in deelpopulaties dan ook bereikt wordt. Opdeling van die omvang naar rato is dus niet de meest efficiënte aanpak, want de steekproeven per deelpopulatie kunnen kleiner, maar dat kan niet zonder veel rekenwerk. Deze verdeling levert hoe dan ook een maximale afwijking op die voldoet aan de uitvoeringsmaterialiteit.

Het recept van Glover, toegepast op het model van Stewart

Het recept dat ik voorstel is als volgt:

1. We gaan uit van een populatie M met materialiteit OM en zetten een steekproef op bij 95 procent betrouwbaarheid en 0 afwijkingen in de steekproef. Die omvang is 3 M/OM (want R = 3).
2. Tweede stap is de tabel die aangeeft, afhankelijk van het aantal deelpopulaties , met welke factor deze steekproefomvang moet worden opgeblazen. Dit is dus niet de factor van Glover, maar een door mij uit het model van Stewart afgeleide factor.
   De formule om de tabel die aan het einde van deze blog staat te maken is:
   GAMMA.INV(betrouwbaarheid; #deelpopulaties;1) / GAMMA.INV (betrouwbaarheid;1;1)
3. Deel deze steekproefomvang naar rato toe aan de (waarschijnlijk in omvang verschillende) deelpopulaties. In plaats van een uitvoeringsmaterialiteit per deelpopulatie wordt dus een gelijk bedrag voor de uitvoeringsmaterialiteit en dus ook voor het steekproefinterval voor alle deelpopulaties gehanteerd.
4. Wie dat wil kan de aggregatieformules van Stewart mee programmeren om te zien dat deze verdeling inderdaad een overall maximale afwijking oplevert die aan de overall materialiteit voldoet.

Verschillen

Een getallenvoorbeeld:

Model van Stewart

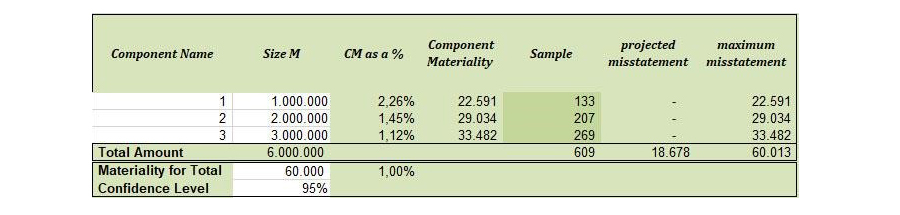
Mijn model

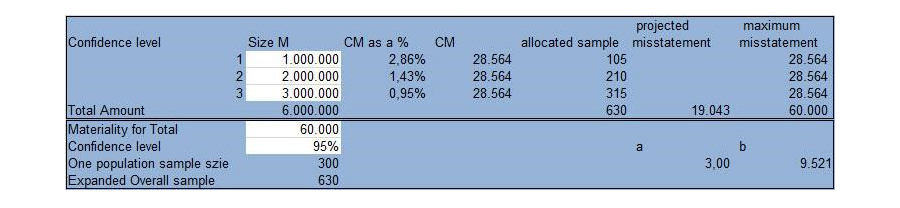
De aanpak van Stewart is natuurlijk methodologisch superieur. Eerst de uitvoeringmaterialiteit bepalen en dan kijken welke steekproef daarvoor nodig is. Gevolg is dan ook dat zijn model rekening kan houden met een vermoedelijke afwijking in deelpopulaties die de omvang van de steekproeven beïnvloedt. Een belangrijk motief om te willen disaggregeren is natuurlijk dat de controleur in sommige deelpopulaties wél, en andere geen afwijkingen verwacht. Mijn model berekent de totale steekproef en rekent terug welke uitvoeringsmaterialiteit daar bij hoort. Dit werkt alleen bij nul (0) afwijkingen, levert meer werk op (630 in plaats van 609 in mijn voorbeeld), maar... is simpel in Excel te berekenen.

Terug naar het beloofde percentage uitvoeringsmaterialiteit ten opzichte van de materialiteit

Uitgaande van de opblaasfactor voor de steekproefomvang (derde kolom) is ook een formule - en dus ook een tabel - te maken voor de uitvoeringsmaterialiteit als percentage van de overall materialiteit.

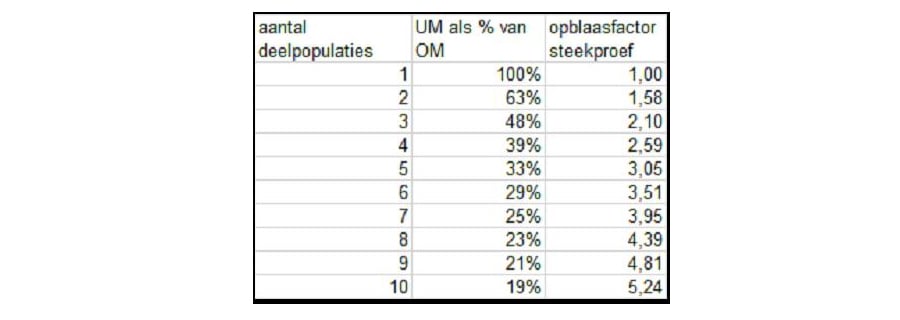
Ten slotte: slecht nieuws voor sommigen en goed nieuws voor iedereen

Eerst het slechte nieuws voor sommigen:
De percentages afslag van overall materialiteit naar uitvoeringsmaterialiteit die uit deze analyse volgen zijn hoger dan de praktijk gewend is. Er is dus sprake van meer werk. Dat geldt overigens alleen voor de private sector, waar materialiteit een bedrag is. 

Dan het goede nieuws voor de publieke sector:
In de publieke sector is materialiteit een percentage en wordt - ondanks dat in COS 600 A43 staat dat dat niet nodig is – het materialiteitspercentage gehandhaafd bij opdeling in deelpopulaties. Voor die accountants is dit verhaal dus goed nieuws!

En dan nog meer goed nieuws:
Deze grotere steekproeven leiden bij nul afwijkingen tot een maximale afwijking onder de overall materialiteit. Vergelijking van de geaccumuleerde afwijking met een percentage van de overall materialiteit in plaats van met het volle bedrag, wat door veel kantoren wordt gedaan als compensatie voor het werken met een vast bedrag aan uitvoeringsmaterialiteit, is dus niet nodig.