De steekproefomvang ontmaskerd - deel 2
Deze tweede column in een serie van vijf bespreekt hoe je zelfstandig de juiste steekproefomvang kunt berekenen.
Niels van Leeuwen
In de vorige column zagen we dat het classificeren van waarnemingen als goed of fout het werken met een discrete verdeling vraagt. Wij behandelden drie discrete verdelingen, namelijk de binomiale, hypergeometrische en Poissonverdeling.
Bij een audit willen we voldoende zekerheid hebben dat er geen materiële hoeveelheid aan fouten of onzekerheden bestaan in onze populatie. De vraag is nu hoe we door middel van statistiek kunnen stellen dat we genoeg waarnemingen hebben gedaan om te spreken van voldoende zekerheid. Om hierachter te komen gaan we in op de vraag: hoe bereken je de steekproefomvang? We beantwoorden deze vraag door eerst het begrip 'voldoende betrouwbaarheid' te duiden in een formule. Vervolgens lossen we deze formule op drie verschillende manieren op:
- Benaderen in Excel voor meerdere verdelingen
- Werken met np-tabellen voor de Poissonverdeling
- Toepassen van de inverse gamma verdeling in Excel als benadering voor de Poissonverdeling
Voldoende betrouwbaarheid
Zoals we in de vorige column vaststelden is het doel van statistiek in de audit om met een beperkt aantal waarnemingen voldoende betrouwbaarheid te verkrijgen dat een populatie vrij is van materiële fouten en onzekerheden. Nu is het woord 'voldoende' natuurlijk onderhevig aan oordeelsvorming. Het hangt dus af van de context wanneer je spreekt over voldoende betrouwbaarheid. Om aan te duiden wat voldoende is gebruiken wij het audit-risk model.
Het audit-riskmodel en statistiek
Hoeveel je moet doen om van voldoende betrouwbaarheid te kunnen spreken hangt af van het geaccepteerde risico op de opdracht. Het audit-riskmodel zegt dat het accountantsrisico (AR) het product is van het inherente risico (IR), het controle risico (CR) en het detectierisico (DR). Het inherente risico is wat er wezenlijk fout kan gaan bij de controle, zonder dat de gecontroleerde organisatie hier iets aan doet. Het controlerisico is het risico dat een materiële fout niet wordt opgemerkt door het stelsel van interne beheersing. Het detectierisico is het risico dat de auditor fouten niet ziet. Hoe meer werk de auditor doet, hoe lager het detectierisico. De drie risico’s moeten gezamenlijk leiden tot een acceptabel laag accountantsrisico. In formulevorm als volgt:
AR = IRxCRxDR
Statistiek kan worden toegepast in de werkzaamheden van de auditor om het detectierisico te verlagen. Hiervoor moet dit detectierisico nog worden vertaald naar een statistische maatstaaf. Het detectierisico is in feite gelijk aan het beta-risico. Het beta-risico is het risico dat een hypothese wordt aangenomen terwijl deze feitelijk moet worden verworpen. Met andere woorden, het beta-risico is in deze situatie het risico dat de auditor een populatie goedkeurt, terwijl er feitelijk sprake is van een materiële fout.
Dit risico moet dus acceptabel laag zijn. Wat acceptabel laag is hangt samen met de hoogte van het inherente en controlerisico, maar als deze buiten beschouwing worden gehouden is het gebruikelijk om hooguit een beta-risico van 5% aan te houden. Dit is hetzelfde als een betrouwbaarheid van 95 procent. We kunnen deze 95 procent betrouwbaarheid invullen in de in de eerste column gepresenteerde formules die de kans op aantal fouten aangeeft voor de drie verdelingen. We willen met 95 procent betrouwbaarheid kunnen stellen dat het maximaal aantal fouten de materialiteit niet overschrijdt. In formulevorm ziet dat er als volgt uit:

De populatieomvang N is een vast gegeven en is de totale omvang waar je een steekproef op berekent. De grote K duidt het aantal fouten in de populatie aan. Deze parameter is onbekend, maar we weten wel dat deze maximaal zo groot mag zijn als de materialiteit. Daarom wordt voor K de materialiteit aangehouden. De kleine k is het aantal fouten dat je tegenkomt in de steekproef. Deze parameter is vooraf ook onbekend, dus bij de planning van een steekproef wordt deze geschat. De foutfactor uitgedrukt in letter p is gelijk aan het aantal fouten in de populatie gedeeld door de populatieomvang. De Griekse letter λ staat voor een gemiddeld aantal fouten per interval en dit is gelijk aan de steekproefomvang vermenigvuldigd met de foutfactor.
In feite is het berekenen van de steekproefomvang een kwestie van het invullen van de parameters tot we die 95 procent betrouwbaarheid hebben bereikt. De parameters N, K, k, p en λ zijn van tevoren bepaald, de enige variabele is n. Deze kun je steeds ophogen tot de uitkomst van de formule uiteindelijk 95 procent aangeeft. We kunnen nu met enkele manieren deze vergelijking oplossen.
Verschillende manieren om de steekproefomvang uit te rekenen
Wij illustreren de manieren van werken aan de hand van twee casussen, die we gedurende deze gehele serie van columns gebruiken. Eén casus, waarbij we geen fouten verwachten, en één waarbij we wel fouten verwachten.
Wanneer we namelijk geen fouten verwachten kunnen we de steekproefomvang ook handmatig uitrekenen, wat we in de volgende column laten zien. Wanneer we wel fouten verwachten kan dat niet handmatig en moeten we een van de andere manieren gebruiken. In beide casussen is de populatieomvang € 1 mln. We hebben een materialiteit van 5 procent, wat neer komt op € 50.000. We willen 95 procent betrouwbaarheid behalen, wat gelijk is aan een maximaal beta-risico van 5 procent. In de eerste casus verwachten we 0 fouten (k1) en in de tweede casus verwachten we 1 fout (k2). Dit kunnen we samenvatten in de volgende variabelen:
- ß = 5%
- N = 1.000.000
- p = 5%
- k1 = 0
- k2 = 1
Benaderen met Excelfuncties
We beginnen met de manier die het meest aansluit bij de bovenstaande formules. Met deze manier vullen we de parameters in een Excel-formule in, waarbij we de steekproef n steeds verhogen tot we onze gewenste betrouwbaarheid hebben behaald. We moeten hiervoor de onderstaande formules in Excel invullen.
|
Verdeling |
Functie |
|
Hypergeometrisch |
95% ≤ 1 - HYPGEOM.VERD(k; n; K; N, 1) |
|
Binomiaal |
95% ≤ 1 - BINOM.VERD(k; n; p; 1) |
|
Poisson |
95% ≤ 1 - POISSON.VERD(k; n*p, 1) |
Wanneer we een benadering doen voor beide scenario's komen we op de volgende steekproefomvang uit:
|
Verdeling |
k1 = 0 |
k2 = 1 |
|
Hypergeometrisch |
59 |
93 |
|
Binomiaal |
59 |
93 |
|
Poisson |
60 |
95 |
In het bijgevoegde Excel-rekenblad kun je dit zelf toepassen in Excel.
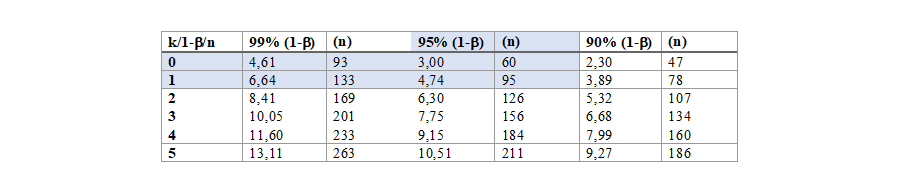
Werken met np-tabellen voor de Poissonverdeling
Een andere relatief eenvoudige manier is het werken met np-tabellen. Deze tabellen geven voor de Poissonverdeling een vaste verhouding in tabel vorm weer. De parameters waar je mee werkt zijn k en 1-b. Door deze te gebruiken kun je de corresponderende np-waarde vinden. De n is eenvoudig te verkrijgen door deze np-waarde te delen door p. Als we deze waardes invullen komen we uit op 3 en 4,74. Als we deze waardes delen door een p van 5 procent komen we uit op een steekproefomvang van 60 en 95, afgerond naar boven.
Toepassen van de inverse gamma verdeling in Excel voor de Poissonverdeling
Wanneer je van een kansberekening weet dat de uitkomst 95 procent moet zijn en alle parameters behalve één bekend zijn, dan kun je de onbekende oplossen. Dit is precies wat de inverse gamma verdeling doet voor de Poissonverdeling. Excel kent geen inverse functie van de Poisson verdeling, maar wel van de gammafunctie. De gamma- en Poissonverdeling zijn gelijk aan elkaar. Het verschil is dat de gammafunctie ook geschikt is voor continue data. Met de inverse gammafunctie kun je dus de np-tabel overslaan en in Excel direct de steekproef terugrekenen. Je gebruikt hiervoor de volgende formule:
|
Verdeling |
Functie |
|
Inverse gamma |
=GAMMA.INV(1-ß;k+1;1)/p |
Ook met deze manier kom je bij k1 en k2 uit op 60 en 95 steken naar boven afgerond. Hoe je deze formule toepast is ook opgenomen in het bijgevoegde Excel-rekenblad.
Kleine verschillen
We hebben nu drie manieren toegepast om tot dezelfde steekproefomvang te komen. Hierbij zien we wel kleine verschillen in omvang. In de eerdere column hebben we de voor- en nadelen van de verschillende manieren besproken. Nu je deze verschillen kent kun je zelf de steekproefomvang op verschillende manieren berekenen en is het hopelijk geen mysterie meer hoe je tot de juiste steekproefomvang komt. Hopelijk geeft dat je meer vertrouwen bij het gebruik van statistiek in de audit.
In de komende column gaan we nog iets dieper in op de gepresenteerde manieren. We bekijken waarom het logisch is dat de inverse functie op een goede steekproefomvang uitkomt. In de vierde column automatiseren we de benaderingswijze in een VBA-script met als doel beter te begrijpen hoe je met behulp van software tot een steekproefomvang komt. In de laatste column laten wij zien hoe je de open software-omgeving JASP kunt gebruiken bij het berekenen van de software van de steekproefomvang.
Bron: Stewart, T. (2012). Technical notes on the AICPA audit guide Audit Sampling. American Institute of Certified Public Accountants, New York, 5-8.
Gerelateerd

Machine learning in de audit: uitschieters bij vastgoedwaardering
Regressie is een vorm van machine learning met als doel het voorspellen van cijfers op basis van een aantal kenmerken. Met open-sourcesoftware kun je zonder programmeerkennis...
Machine learning in de audit: voorspellen van klantverloop
Het doel van machine learning is om voorspellingen te maken aan de hand van data. Binnen dit veld worden doorgaans drie hoofdtoepassingen onderscheiden: classificatie,...

De steekproefomvang ontmaskerd - deel 5
In vorige columns hebben we verschillende manieren besproken om tot een steekproefomvang te kunnen komen. Deze column is de laatste van de serie waarin we verschillende...

De steekproefomvang ontmaskerd - deel 4
Een accountant die gebruikmaakt van software om een steekproefomvang te berekenen, moet zeker weten dat die software dat goed doet. Daarvoor moet je de rekenmethode...

Symposium: Machine Learning in de audit
Hoe is het momenteel gesteld met de toepassing van Machine Learning in de audit? Aankondiging van een symposium.
